Tour de Chemie – Mol und Co

Die Tour de Chemie erstreckt sich über vier Etappen und soll dir wichtige Grundkenntnisse zum chemischen Rechnen vermitteln. Dieses Wissen wirst du immer wieder benötigen! Am Ende jeder Etappe kannst du eine Etappenprüfung absolvieren. Beim bestehen der Prüfung darfst du zur nächsten Etappe fahren. Und nun, viel Erfolg dabei ;-).

Etappe 1: Die Atom- und Molekülmasse

Schauen wir uns einmal die folgende Reaktion an. Dort ist zu erkennen, dass ein Kohlenstoff-Atom mit einem Sauerstoff-Molekül zu einem Kohlenstoffdioxid-Moleküle reagiert. Wie alles um uns herum haben auch Atome und Moleküle ein Gewicht.

Mit Hilfe des Periodensystems können wir das Gewicht ermitteln. Die Masse eines einzelnen Atoms, also die Atommasse, ist eine wichtige Information. Deshalb ist im Periodensystem neben dem Symbol und der Ordnungszahl auch die Atommasse angegeben. Aus Gründen der Übersichtlichkeit wird dabei die Atommasse nicht in der Einheit „Gramm (g)“ oder „Kilogramm (kg)“, sondern in der „atomaren Masseneinheit u“ angegeben.

Mit Hilfe der Informationen können wir die Masse eines Kohlenstoffdioxid-Atoms berechnen, indem wir die Massen der einzelnen Atome zusammenaddieren (wir runden die Atommassen auf 12 u bzw. 16 u ab, bzw. auf):

\( \mathbf{m_{(CO_2 -Molekül\,(u))}}=m_{(C-Atom\,(u))}+2 \cdot m_{(O-Atom\,(u))}= 12 \, u +16 \, u= \mathbf{44\,u}\)

Ein Kohlenstoffdioxid-Atom hat die Masse von 44 u. Sollten wir für ein Versuch die Masse abwiegen wollen, zeigen uns die Waagen allerdings nur die Masse in Gramm an. Mit Hilfe der folgenden Angabe, können wir die Atommasse in Gramm angeben:

\( \mathbf{m_{(CO_2 -Molekül\,(u))}}=44\,u\)

\( \mathbf{1\,u} = 1,66 \cdot 10^{-24}\,g \)

\( \mathbf{m_{(CO_2 -Molekül\,(g))}}= 44\,u \cdot 1,66 \cdot 10^{-24}\,g = \mathbf{7,304 \cdot 10^{-23}\,g} \)

Ich denk es wird deutlich, dass ein CO₂-Molekül ein sehr geringes Gewicht aufweist.

Hilfe zum Umgang mit der Exponentialschreibweise

Zur Erinnerung schauen wir uns nochmal den Umgang mit der Exponentialschreibweise ein. Zahlen wirken häufig kompliziert, wenn der Zusatz \( \cdot10^{-24}\) oder andere Exponenten vorhanden sind. Dabei helfen uns die Exponenten dabei, dass wir nicht so viele Zahlen per Hand hinschreiben müssen. Wir verdeutlichen uns das an einem Beispiel:

Die Zahl 1000 können wir auch wie folgt ausdrücken:

\( 1000 = 1 \cdot10^{3}\)

Die Zahl 540000 können wir auch wie folgt ausdrücken:

\( 540000 = 5,4 \cdot10^{5}\)

Die Zahl 0,0001 können wir auch wie folgt ausdrücken:

\( 0,0001 = 1 \cdot10^{-4}\)

Absolviere deine erste Etappenprüfung. Du musst mind. 80% erreichen, um in die nächste Etappe gelangen zu können. Solltest du die Prüfung nicht schaffen, schaue dir deine Fehler an und versuche es erneut.
Du kannst deine Antwort nach jeder Auswahl überprüfen oder du erhältst nach der Beantwortung aller Fragen eine Auswertung.

Etappe 2: Die Abzähleinheit Mol

In der letzten Etappe haben wir ermittelt, wie viel ein Kohlenstoffdioxid-Molekül wiegt. Dabei ist uns aufgefallen, dass das Gewicht sehr gering ist. In der Schule- oder im Universitätslabor können wir ein solches Gewicht nicht abwiegen und das würde auch kein Sinn ergeben.

Für uns als Chemiker ist es aber wichtig zu wissen, wie viele Atome bzw. Moleküle wir am Anfang benötigen, damit eine bestimmte Menge an Kohlenstoffdioxid-Molekülen am Ende auch rauskommen. Ihr könnt euch das sicherlich schon denken, in einem Gramm Kohlenstoff ist eine unvorstellbar große Zahl an Kohlenstoff-Atomen zu finden. Nämlich etwa: 50 Trilliarden Kohlenstoff-Atome. Diese Zahl ist sehr unhandlich zu handhaben!

Aus diesem Grund wurde eine neue physikalische Größe, die Stoffmenge n eingeführt. Die wir uns als nächstes genauer anschauen wollen.

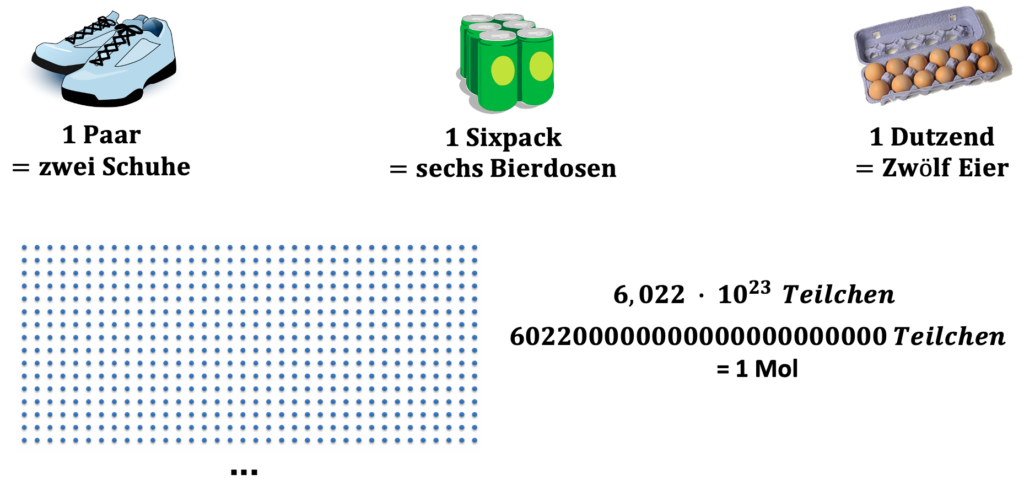
Mit Hilfe der Abbildung kannst du erkennen, dass ein Begriff immer eine gewisse Anzahl von etwas beschreibt. 1 Paar Schuhe entsprechen 2 einzelnen Schuhen oder ein Sixpack-Bier entspricht 6 einzelnen Flaschen und dieses Prinzip wenden wir in der Chemie auch an. Statt vom „Sixpack“ zu sprechen reden wir von der Einheit „Mol“. Ein Mol entsprechen 602200000000000000000000 Teilchen (z.B. Atome oder Moleküle). Das ist eine seeehr große Zahl, die wir auch mit Hilfe der Exponentialschreibweise ausdrücken können: \( 6,022 \cdot 10^{23}\,Teilchen\)

Falls du Wissen möchtest, wieso man die Zahl 602200000000000000000000 für ein Mol gewählt hat, dann tippe hier.

Um diese Frage zu beantworten, wird nun die Masse von einem Mol Kohlenstoff-Atomen in der Einheit „Gramm“ berechnet. Wir wissen bereits, dass die Atommasse von einem Kohlenstoff-Atom 12 u beträgt. Nun wollen wir ausrechnen, wie viel Gramm 1 Mol Kohlenstoff-Atome wiegen. Dazu setzten wir die Anzahl an Teilchen ein, die sich in einem Mol (\( 6,022 \cdot 10^{23})\) befinden und multiplizieren das mit dem Gewicht von einem Kohlenstoff-Atom (in u) und rechnen das Gewicht in die Einheit Gramm um.

\( \mathbf{m_{(Kohlenstoff -Atom\,(g))}}= 12\,u \cdot 6,022 \cdot 10^{23} \cdot 1,66 \cdot 10^{-24}\,g\)

\( \mathbf{m_{(Kohlenstoff -Atom\,(g))}}= 12\,g\)

Als Ergebnis für die Masse von einem Mol Kohlenstoff-Atome in der Einheit „Gramm“ erhält man den gleichen Zahlenwert, wie er sich für die Masse eines Kohlenstoff-Atoms in der Einheit „u“ ergibt. Und das ist kein Zufall. Für jedes Element im Periodensystem ist die angegebene Atommasse „u“ vom Zahlenwert her identisch mit der Masse eines Mols der Element-Atome in der Einheit „Gramm“!

Wir erkennen also, wie sinnvoll die Einheit Mol ist und wir wissen, dass wir im Labor mit der Einheit Gramm arbeiten. Eine weitere physikalische Größe ist die molare Masse M. Mit Hilfe der molaren Masse kann man zwischen der Stoffmenge und dem Gewicht umrechnen. Die molare Masse M wird in der Einheit (gelesen: Gramm pro Mol) angegeben und beschreibt das Gewicht von Atomen in Gramm bezogen auf 1 Mol. Die molare Masse lässt sich leicht mit Hilfe des Periodensystems ermitteln, indem man die Atommasse verwendet, jedoch in der Einheit \(\frac{g}{mol}\). Für Kohlenstoff und Sauerstoff lautet die molare Masse \((M)\) .

\(M_{(C)}=12\,\frac{g}{mol}\) beziehungsweise \(M_{(O)}=16\,\frac{g}{mol}\)

Im nächsten Schritt wollen wir die molare Masse von \(CO_2\) berechnen, diese lässt sich nicht aus dem PSE ablesen, da sich aus den Elementen Kohlenstoff und Sauerstoff zusammensetzt. Wir erinnern uns an die Reaktionsgleichung: \(C+O_2 \longrightarrow\:CO_2\)

\(M_{(CO_2)}=M_{(C)}+ 2 \cdot M_{(O)} = 12\,\frac{g}{mol}+2\cdot 16\,\frac{g}{mol}=44\,\frac{g}{mol} \)

Eine Formel für alle Fälle – Mit Hilfe der folgenden Formel können alle drei Größen miteinander in Beziehung gesetzt werden. Du solltest dir die Formel unbedingt merken.
Die Stoffmenge lässt sich wie folgt berechnen:

\(n=\frac{m}{M}\)

n = Stoffmenge in der Einheit mol
M = molare Masse in der Einheit \(\frac{g}{mol}\)
m = Masse in Gramm

Beispielaufgabe zur Anwendung der Formel

In einem Experiment sollen 2 Mol Schwefel mit Sauerstoff reagieren. Berechne, wie viel Gramm Schwefel dafür abgewogen werden müssen?

Für das Experiment müssen also 64 Gramm abgewogen werden. Je nachdem wie die Frage lautet oder welche Angaben vorhanden sind, lässt sich die Formel umstellen:

\(M=\frac{m}{n}\)

\(n=\frac{m}{M}\)

\(m=n \cdot m\)

Absolviere deine zweite Etappenprüfung. Du musst mind. 80% erreichen, um in die nächste Etappe gelangen zu können. Solltest du die Prüfung nicht schaffen, schaue dir deine Fehler an und versuche es erneut.
Du kannst deine Antwort nach jeder Auswahl überprüfen oder du erhältst nach der Beantwortung aller Fragen eine Auswertung.

Etappe 3: Die Stoffmengenkonzentration

In der Etappe 3 beschäftigen wir uns mit dem Begriff Konzentration. Damit wir eine Konzentration angeben können, benötigen wir einen Stoff (z.B. Zucker), der in einem Lösungsmittel (z.B. Wasser) gelöst ist. Mit Hilfe der Konzentration können wir angeben, welche Stoffmenge (in mol) eines Stoffes in einem bestimmten Volumen (z.B. 1 Liter) Wasser gelöst ist.

Die nachfolgende Abbildung soll den Konzentrationsbegriff verdeutlichen. In einem Becherglas wurde 1 mol Zucker in einem Liter Wasser aufgelöst. Die Stoffmengenkonzentration beträgt: \(1 \frac{mol}{L}\)

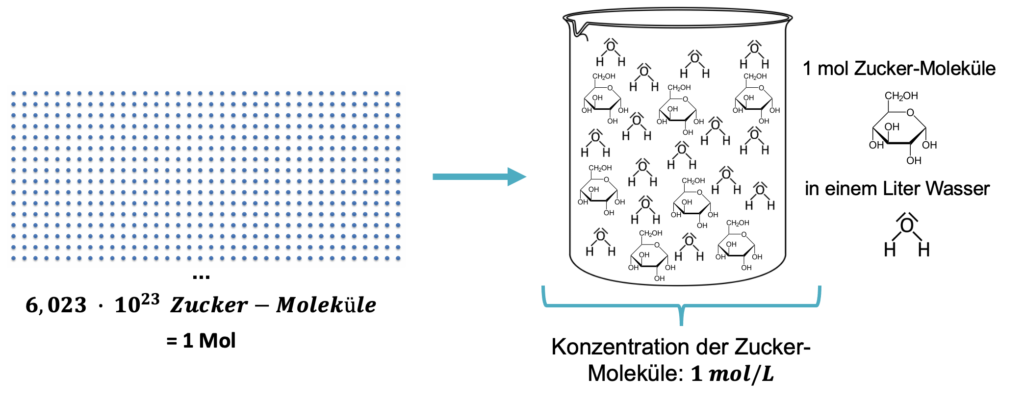
Die Stoffmengenkonzentration lässt sich wie folgt berechnen:

\(c=\frac{n}{V}\)

c = Stoffmengenkonzentration in der Einheit \(\frac{mol}{L}\)
n = Stoffmenge in der Einheit mol
V = Volumen in der Einheit Liter

Absolviere deine dritte Etappenprüfung. Du musst mind. 80% erreichen, um in die nächste Etappe gelangen zu können. Solltest du die Prüfung nicht schaffen, schaue dir deine Fehler an und versuche es erneut.
Du kannst deine Antwort nach jeder Auswahl überprüfen oder du erhältst nach der Beantwortung aller Fragen eine Auswertung.

Etappe 4: Das molare Volumen von Gasen

In dieser Etappe wollen wir uns mit dem molaren Volumen (V_M) beschäftigen. Mit dem molaren Volumen wird ausgedrückt, welches Volumen Gase einnehmen. Das Volumen wird in der Einheit Liter angegeben. Die Abbildung zeigt drei unterschiedliche Ballons die mit unterschiedlichen Gasen (Wasserstoff, Sauerstoff und Kohlenstoffdioxid) befüllt wurden. In jedem Ballon befinden sich 1 Mol des entsprechenden Gases.

Bei dem Vergleich der Ballons fällt uns auf, dass jeder Ballon die gleiche Größe hat, obwohl es sich um unterschiedliche Gase handelt. Jeder Ballon fasst ein Volumen von 22,4 Litern. Die Gemeinsamkeit ist allerdings kein Zufall! Ein Mol eines beliebigen Gases nimmt immer bei 0°C und Normaldruck ein Volumen von 22,4 Litern ein. Aus dem Ergebnis lässt sich das molare Volumen (V_M) formulieren:

\(V_{M(Gas)}=22,4\frac{L}{mol}\)

Damit lässt sich über das Volumen eines beliebigen Gases direkt auf die vorliegende Stoffmenge n schließen. Es gilt:

\(n_{(Gas)}=\frac{V_{Gas}}{V_{M(Gas)}}=\frac{V_{Gas}}{22,4 \frac{L}{mol}}\)

Schauen wir uns ein Übungsbeispiel an:

In einem Ballon befindet sich das Gas Methan (CH₄). Das Volumen beträgt 28 Liter. \(V_{CH_4}=28 Liter\)

Berechne die Stoffmenge n die sich im Ballon befindet.

\(n_{(CH_4)}=\frac{V_{Gas}}{V_{M(Gas)}}=\frac{28 L}{22,4 \frac{L}{mol}}=1,25\,mol\)

Ergebnis: Im Ballon befinden sich 1,25 mol Methan \((CH_4)\).

Ach übrigens… Mit steigender Temperatur nimmt das Volumen der Gase übrigens zu. So nimmt ein Mol eines beliebigen Gases bei Raumtemperatur (20°C) ein Volumen von etwa 24 Litern ein.

Absolviere deine vierte Etappenprüfung. Du musst mind. 80% erreichen, um in die nächste Etappe gelangen zu können. Solltest du die Prüfung nicht schaffen, schaue dir deine Fehler an und versuche es erneut.
Du kannst deine Antwort nach jeder Auswahl überprüfen oder du erhältst nach der Beantwortung aller Fragen eine Auswertung.

Herzlichen Glückwunsch Du hast die Tour de Chemie erfolgreich absolviert.
Im folgenden findest du nochmal die gelernten Formeln.

\(M=\frac{m}{n}\)

\(c=\frac{n}{V}\)

\(n=\frac{V_{Gas}}{V_M}\)